L’articolo definisce formule di calcolo per la determinazione della distanza minima di installazione di file di pannelli fotovoltaici, su suolo piano o collinare, e della altezza di installazione, in caso di pendenza del terreno variabile o impossibilità di rispetto della distanza minima.
In caso di installazione di pannelli fotovoltaici su un terreno inclinato rispetto all’orizzontale, la distanza di installazione tra le file che costituiscono il campo fotovoltaico può essere ridotta rispetto alla installazione in piano, sfruttando l’effetto della pendenza, ma non può scendere al di sotto di un valore minimo che segna l’inizio del cosiddetto fenomeno di ombreggiamento.
Un errore nella definizione della distanza minima potrebbe portare alcune file di pannelli in ombra a causa della fila precedente, con conseguente forte riduzione della produzione di energia elettrica. Per evitare tale fenomeno e le relative perdite economiche, le file di pannelli devono essere disposte a una distanza tra di loro tale che l’ombra aggettata da ciascun pannello in nessun caso raggiunga la fila successiva, come illustrato in fig.1, ma sia contenuta nell’area che separa le file di pannelli.

Al fine di analizzare la possibilità del fenomeno di ombreggiamento, si considera la rappresentazione schematica della disposizione dei pannelli su un piano inclinato (fig.2), che potrebbe rappresentare la falda di un tetto così come il profilo di una collina, dove alle lettere sono attribuiti i seguenti significati:
- L è la lunghezza della sezione del pannello in esame;
- d è la distanza minima del pannello successivo;
- β è l’angolo di inclinazione del pannello rispetto all’orizzontale;
- γ è l’angolo di inclinazione del terreno rispetto all’orizzontale;
- δ è l’angolo di declinazione al solstizio d’inverno.
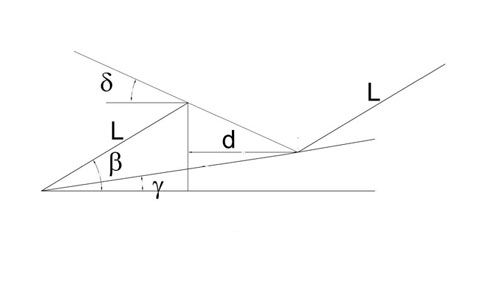
La grandezza d rappresenta la distanza dalla proiezione del pannello sull’asse orizzontale alla quale i raggi solari al solstizio di inverno colpiscono il terreno e, pertanto, costituisce la distanza minima tra le file di pannelli per evitare il fenomeno dell’ombreggiamento.
L·sen(β)= d·tg(δ) + d·tg(γ) + L·cos(β)·tg(γ)
In particolare l’uguaglianza si ricava esprimendo la proiezione sull’asse verticale del pannello (primo membro dell’eguaglianza) come sommatoria dei cateti verticali dei tre triangoli costituiti, rispettivamente da:
- la verticale per l’estremità più alta del pannello, l’orizzontale e il piano di installazione;
- la verticale per l’estremità più alta del pannello, la distanza minima d e il piano di installazione;
- la verticale per l’estremità più alta del pannello, la distanza minima d e il raggio solare, inclinato secondo le ore 12 del solstizio di inverno, che aggetta ombra dall’estremità più alta del pannello.
Applicando, a ciascuno dei tre triangoli considerati, i teoremi di trigonometria relativi alla relazione tra cateti nei triangoli rettangoli (“un cateto è uguale all’altro cateto per la tangente dell’angolo opposto al primo cateto”), si ottengono i tre addendi a secondo membro.
Dalla uguaglianza precedente, si ricava la distanza minima d in funzione degli angoli e della lunghezza dei pannelli, come riportato nella formula seguente:
d = [sen(β)-cos(β)·tg(γ)]/[tg(δ)+tg(γ)]·L
La formula è particolarmente utile in caso di installazione dell’impianto sul profilo di una collina con pendenza variabile lungo l’asse NS. In tal caso, a diversi valori di pendenza, lungo il campo fotovoltaico, corrispondono diverse distanze minime tra i pannelli.
Distanza pannelli fotovoltaici e pendenza del terreno
A titolo di esempio, in fig.3, si riportano le distanze minime in funzione della pendenza del terreno calcolate considerando un angolo di declinazione solare pari a 24,3° e i pannelli inclinati di 31° rispetto all’orizzontale.
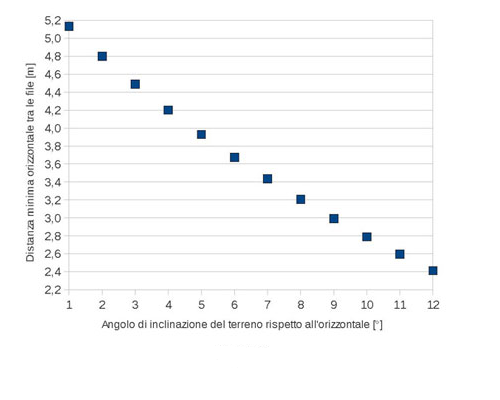
La distanza di 2,8 metri, corrispondente, nel caso in esame, a un’inclinazione del terreno di 10°, potrebbe essere assunta come distanza minima di installazione, atta a permettere il passaggio di mezzi di lavoro, anche su campi con pendenza del terreno variabile, adottando l’accortezza di ricorrere all’utilizzo di sostegni ad altezza variabile: il rispetto della distanza minima sarà sufficiente a evitare l’ombreggiamento anche per pendenze maggiori, mentre per pendenze del terreno inferiori sarà necessario intervenire sull’altezza dei sostegni.
L’installazione di un pannello a distanza dalla fila precedente inferiore alla distanza minima è rappresentata in fig.4, dove alla rappresentazione schematica già esaminata si aggiungono il dislivello h necessario ad evitare il fenomeno dell’ombreggiamento e la distanza D tra le proiezioni dei pannelli sul piano orizzontale.
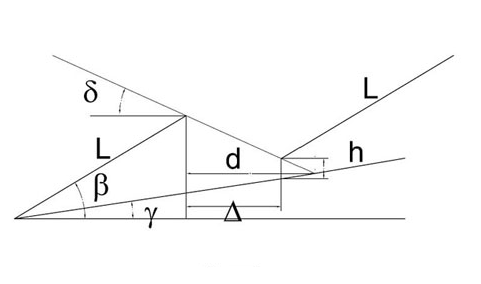
Applicando i principi della trigonometria alla rappresentazione di cui sopra, si ottiene la seguente eguaglianza
h = (d-Δ)·[tg(δ)+tg(γ)] con Δ
La formula permette di calcolare il dislivello di altezza h da dare al sostegno di un pannello rispetto al pannello precedente, in funzione della pendenza g del terreno, in caso di installazione a distanza Δ inferiore alla distanza minima d.
Nella fig.5, si rappresentano i dislivelli di altezza dei sostegni necessari a garantire l’assenza di ombreggiamento tra i pannelli, in caso di installazione a 2,8 metri di distanza e pendenza del terreno inferiore a 10°.
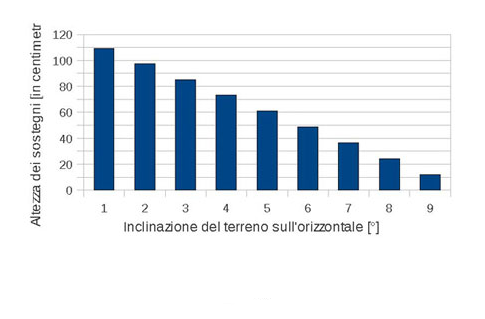
È da specificare che l’altezza riportata in tabella può ridursi nel caso di installazione dei pannelli a distanza maggiore di quella minima, così come è da considerare che l’innalzamento di un sostegno non sempre comporta la necessità di innalzamento del sostegno successivo, proprio in relazione alla variazione di pendenza del terreno.
Si noti che, in caso di installazione su terreno piano (γ=0), le formule precedenti si riducono alle seguenti:
d = [sen(β)/tg(δ)]·L
h = (d-Δ)·tg(δ) con Δ
La corretta disposizione dei pannelli può, in fine, verificarsi graficamente rappresentando il fascio di raggi solari incidente con una linea che, a partire dall’estremità superiore del pannello, va a cadere sul terreno formando con l’orizzontale un angolo pari all’angolo di declinazione al solstizio d’inverno e delimitando l’area d’ombra dovuta al pannello.
Nella fig.6 si riporta un esempio di sezione ottenuto con seguenti dati:
- pendenza del terreno variabile da 6,9° a 11,8° con alternanza di andamenti crescenti e decrescenti;
- pannelli sono installati ad una distanza di 3,3 m (corrispondente alla distanza minima per una pendenza di circa 8°).
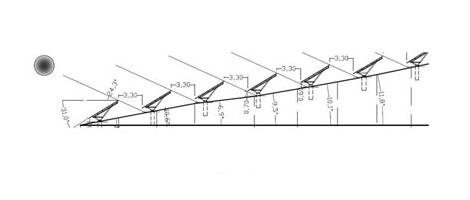
In conclusione, le formule ottenute si ritengono utili per l’ottimizzazione degli spazi nelle installazioni di impianti fotovoltaici su terreni collinari o per un rapido adattamento, in fase di installazione, a compensazione di eventuali variazioni di pendenza del terreno, rispetto alla pendenza di riferimento.
Articolo di Nicola Benedetti, ingegnere elettrico, libero professionista
C.so Vittorio Emanuele II n. 10, 65121 Pescara
tel: (+39) 0859431315 – fax: (+39) 0857992435
skype: n-benedetti – e-mail: n-benedetti@n-b.it
www.n-b.it
Articolo originariamente pubblicato su Ingegneri.cc
Consigliamo
Sistemi Fotovoltaici
Il volume è una guida completa i) alla progettazione degli impianti fotovoltaici grid-connected, anche dotati di sistemi di accumulo, ii) alla presentazione degli interventi di manutenzione per ottimizzarne le prestazioni, iii) alla trattazione delle tematiche inerenti agli ammodernamenti tecnologici eseguiti su impianti in esercizio (revamping e repowering), iv) alla generazione distribuita residenziale ed industriale e ai sistemi di potenza multimegawatt ed utility-scale. Il testo mostra l’architettura di un sistema fotovoltaico, fornendone gli elementi necessari per il corretto dimensionamento impiantistico, descrivendone approfonditamente l’ingegneria di sistema: dal gruppo di generazione fino al punto di connessione alla rete elettrica. Il volume è aggiornato alla normativa elettrica vigente, anche con particolare attenzione alle recenti disposizioni normative in tema di implementazione dei sistemi di accumulo all’interno del sistemo elettrico. Una parte del volume è dedicata all’esercizio in parallelo con la rete elettrica dei sistemi fotovoltaici, descrivendone le tipologie di connessione in bassa, media ed alta tensione, gli aspetti progettuali e l’iter TICA – dalla richiesta di connessione inoltrata al gestore di rete, fino alla realizzazione delle opere di rete. Il testo mostra le operazioni di manutenzione ordinaria standard, fino ad arrivare all’analisi termografica realizzata con droni. Sono illustrati casi di impianti fotovoltaici “under performing”, e mostrati nel dettaglio esempi di malfunzionamenti o guasti di moduli fotovoltaici ed altri componenti di impianto che comportano riduzione del performance ratio. Il testo mostra tutti gli adempimenti burocratici a cui occorre ottemperare al fine di evitare sanzioni economiche e garantire il mantenimento del diritto all’incentivo e alle convenzioni GSE per impianti incentivati e impianti fotovoltaici eserciti in grid/market parity. Di prezioso ausilio pratico risultano essere le 15 relazioni tecniche di impianti fotovoltaici, complete di schemi elettrici e calcoli progettuali – rilasciati nello spazio web a disposizione del lettore. Alessandro CaffarelliIngegnere aerospaziale, è CTU presso il Tribunale Ordinario di Roma. Ha progettato e diretto lavori per oltre 700 MW di impianti fotovoltaici ed eolici. È socio fondatore di Intellienergia ed attualmente Business Development Manager per EF Solare Italia.Giulio de SimoneIngegnere meccanico, Ph.D. in Ingegneria dell’Energia e Ambiente. È socio fondatore e CEO di Intellienergia. Ha progettato e diretto lavori per oltre 500 MW di impianti di produzione di energia rinnovabile.Angelo PignatelliIngegnere elettronico, Ph.D. in Ingegneria dei Sistemi, PMP presso il Project Management. Ha progettato e diretto lavori per oltre 200 MW di impianti di produzione di energia rinnovabile. Kostantino TsolakoglouIngegnere aerospaziale, MSc, si occupa di sviluppo, progettazione, asset management e O&M di impianti utility scale. È Head of Engineering presso una delle maggiori realtà europee in ambito fotovoltaico. Gli autori sono docenti per conto dell’Ordine degli Ingegneri della Provincia di Roma.
Alessandro Caffarelli, Angelo Pignatelli, Giulio de Simone, Konstantino Tsolakoglou | 2021 Maggioli Editore



















Scrivi un commento
Accedi per poter inserire un commento